Câu hỏi:
3 năm trước
Đáy của hình chóp $S.ABCD$ là một hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt đáy và có độ dài là \(a\). Thể tích khối tứ diện \(S.BCD\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
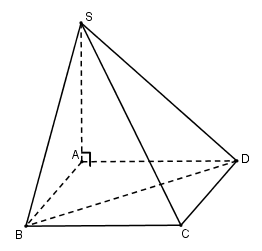
Ta có: \({S_{\Delta BCD}} = \dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{2}{a^2}\)
\({V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\)
- Bước 2: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án B vì không đọc kí đề, coi \(ABCD\) đáy và tính diện tích đáy \(S = {a^2}\) là sai.
Cách làm khác: Các em có thể nhận xét \({V_{S.BCD}} = \dfrac{1}{2}{V_{S.ABCD}}\) nên có thể tính \({V_{S.ABCD}}\) rồi suy ra đáp án.



