Câu hỏi:
2 năm trước
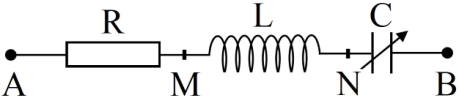
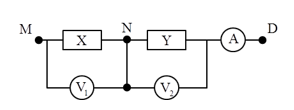
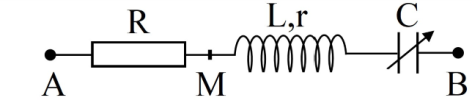Đặt một điện áp xoay chiều vào hai đầu đoạn mạch nối tiếp gồm cuộn dây có điện trở \(R\), hệ số tự cảm \(L\) và tụ điện có điện dung \(C\) thay đổi được. Ban đầu \(C = {C_1}\), khi đó điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch, điện áp hai đầu cuộn dây có giá trị hiệu dụng là \(60{\rm{ }}V\) và nhanh pha hơn điện áp hai đầu đoạn mạch một góc \(\dfrac{\pi }{3}\) . Giảm dần điện dung của tụ đến giá trị \(C = {C_2}\) thì hiệu điện áp hiệu dụng hai đầu tụ điện và điện áp hiệu dụng hai đầu cuộn dây bằng \(10V\). Khi đó điện áp hiệu dụng hai đầu cuộn dây có giá trị gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: b
+ Khi \(C = {C_1}\) , \(u\) cùng pha với \(i\), trong mạch có cộng hưởng.
\({U_{AB}} = {U_R};{U_{LR}} = {\rm{ }}60V\)
\(\begin{array}{l}\tan \varphi = \frac{{{U_L}}}{{{U_R}}} = \tan {60^0} = \sqrt 3 \to {U_L} = \sqrt 3 {U_R}\\{U_{LR}} = \sqrt {U_L^2 + U_R^2} = 60\\ \to \left\{ \begin{array}{l}{U_L} = 30\sqrt 3 V\\{U_R} = 30V\end{array} \right.\end{array}\)
\(\dfrac{R}{{{Z_L}}} = \dfrac{{{U_R}}}{{{U_L}}} = \dfrac{1}{{\sqrt 3 }} \Rightarrow {Z_L} = \sqrt 3 R = {Z_{{C_1}}}\)
\({U_{AB}} = {U_R} = 30V\)
+ Khi\(C = {C_2}\) thì \({U_{{C_2}}} - {U_{LR'}} = 10V\)
Đặt \({U_{LR'}} = a \to {U_{{C_2}}} = a + 10\) Biết \({U_{AB}} = 30V\), ta có : \(\begin{array}{l}U_{_R}^2 + {\left( {{U_L}^\prime - {U_{{C_2}}}} \right)^2} = {30^2} \Leftrightarrow U_{_R}^2 + U_{_L}^2 + U_{{C_2}}^2 - 2.{U_L}^\prime .{U_{{C_2}}} = 900\\ \Leftrightarrow U_{_{LR}}^2 - 2.{U_L}^\prime .{U_{{C_2}}} + {U^2}_{{C_2}} = 900(*)\end{array}\)
Mặt khác, vì \({Z_L} = \sqrt 3 R \Rightarrow {U_L}^\prime = \sqrt 3 {U_R}^\prime \)
\(\begin{array}{l}{U_{LR'}} = \sqrt {{U_R}{'^2} + {U_L}{'^2}} = 2{U_R}' = \dfrac{2}{{\sqrt 3 }}{U_L}'\\ \Rightarrow {U_L}^\prime = \dfrac{{\sqrt 3 }}{2}{U_{LR}}^\prime \end{array}\)
Thay \({U_{LR'}} = a;{U_{{C_2}}} = a + 10\) vào biểu thức (*) ta được : \(\begin{array}{l}{a^2} + {(a + 10)^2} - 2.(a + 10).\dfrac{{\sqrt 3 }}{2}a = 900\\ \Rightarrow (2 - \sqrt 3 ){a^2} + (20 - 10\sqrt 3 )a - 800 = 0 \Leftrightarrow \left\{ \begin{array}{l}{a_1} = 49,86V\\{a_2} = - 59,86V\end{array} \right.\end{array}\)
Chọn đáp án gần giá trị \(a{\rm{ = }}49,86V = 50V\)
Hướng dẫn giải:
+ Vẽ giản đồ véc-tơ
+ Sử dụng biểu thức tính \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{{{U_L} - {U_C}}}{{{U_R}}}\)
+ Hiệu điện thế hiệu dụng của mạch: \({U^2} = U_R^2 + {\left( {{U_L} - {U_C}} \right)^2}\)
+ Sử dụng định luật Ôm, chú ý điều kiện cộng hưởng.
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
