Câu hỏi:
2 năm trước
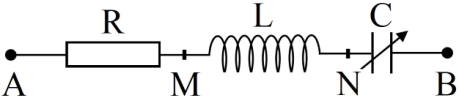
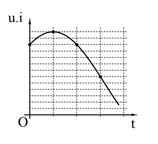
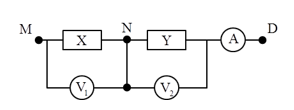
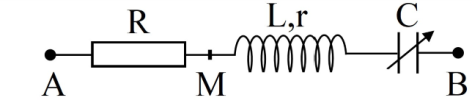Đặt một điện áp xoay chiều \(u = U\sqrt 2 c{\rm{os}}\omega t(V)\) , trong đó \(U\) không đổi, \(\omega \) thay đổi được vào một đoạn mạch gồm có điện trở \(R\), tụ điện và cuộn cảm thuần có hệ số tự cảm \(L = \dfrac{{1,6}}{\pi }H\) mắc nối tiếp. Khi \(\omega = {\omega _0}\) thì công suất trên đoạn mạch đạt cực đại và bằng \(732W\). Khi \(\omega = {\omega _1}\) hoặc \(\omega = {\omega _2}\) thì công suất tiêu thụ trên đoạn mạch bằng nhau và bằng \(300W\). Biết \({\omega _1} - {\omega _2} = 120\pi \left( {rad/s} \right)\). Giá trị của \(R\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: c
+ Khi \(\omega {\rm{ }} = {\rm{ }}{\omega _0}\) công suất trên mạch đạt cực đại: \(\) \(\omega _0^2 = \dfrac{1}{{LC}}\) , \({P_{m{\rm{ax}}}} = \dfrac{{{U^2}}}{R} = 732 \Rightarrow {U^2} = 732R(*)\)
+ Khi \(\omega = {\omega _1}\) và \(\omega = {\omega _2}\) ; \({\omega _1}-{\omega _2} = 120\pi \) thì công suất tiêu thụ trên đoạn mạch bằng nhau :
$\begin{array}{l}{P_1} = {P_2} = P = 300{\rm{W}}\\ \Leftrightarrow \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{L1}} - {Z_{C1}}} \right)}^2}}} = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}}}\\ \Rightarrow {\omega _1}{\omega _2} = \dfrac{1}{{LC}} = \omega _0^2\end{array}$
+ Ta có :
$\begin{array}{l}{Z_{L1}} - {Z_{C1}} = {\omega _1}L - \dfrac{1}{{{\omega _1}{C_1}}} = {\omega _1}L - \dfrac{1}{{\dfrac{{\omega _0^2}}{{{\omega _2}}}C}}\\ \leftrightarrow {\omega _1}L - \dfrac{{{\omega _2}}}{{\omega _0^2C}} = {\omega _1}L - \dfrac{{{\omega _2}}}{{\dfrac{1}{{LC}}C}}\\ = {\omega _1}L - {\omega _2}L = \left( {{\omega _1} - {\omega _2}} \right)L = 120\pi \dfrac{{1,6}}{\pi } = 192\\ \Rightarrow {Z_{L1}} - {Z_{C1}} = 192(**)\end{array}$
+ Công suất tiêu thụ : \(P = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{L1}} - {Z_{C1}}} \right)}^2}}} = 300 \Rightarrow 300{R^2} + 300{\left( {{Z_{L1}} - {Z_{C1}}} \right)^2} = {U^2}R(***)\)
Từ (*) ; (**) ; (***) ta suy ra: \(300{R^2} + {300.192^2} = 732{R^2} \Rightarrow R = 160\Omega \)
Hướng dẫn giải:
Bài toán mạch điện R, L, C mắc nối tiếp có ω thay đổi
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
