Câu hỏi:
2 năm trước
Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol \((P)\). Biết rằng đạn của máy bắn đá bắn xa \(100\;{\rm{m}}\) và tại thời điểm đạn cao \(60\;{\rm{m}}\) thì đạn cách điểm bắn \(80\;{\rm{m}}\).
Vị trí đạn bay cao nhất cách mặt đất bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: d
Bước 1: Đặt hệ trục tọa độ. Gọi \((P):y = a{x^2} + bx + c\). Tìm (P).
Đặt hệ trục như hình vẽ.
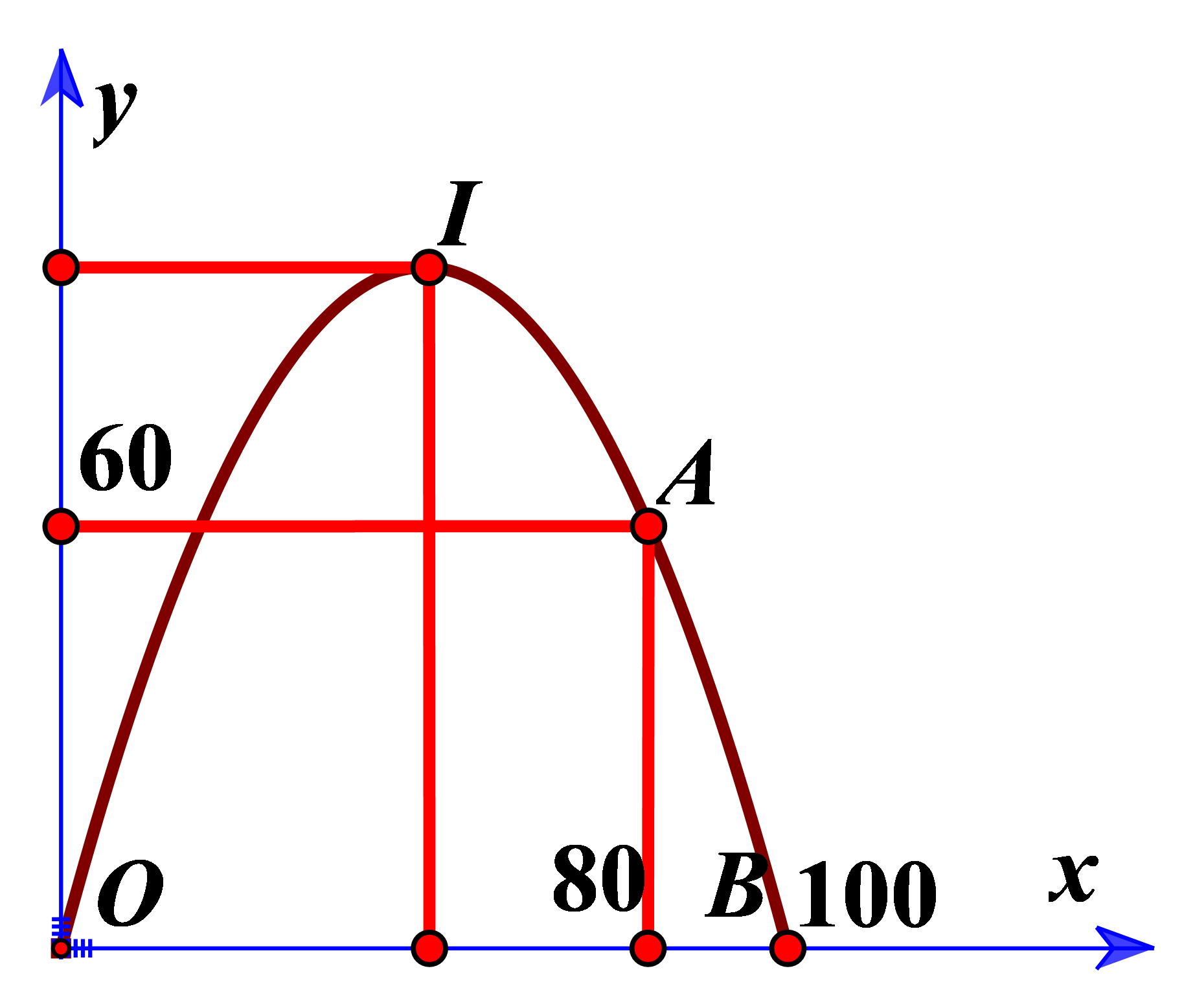
Gọi \((P):y = a{x^2} + bx + c\).
Ta có \((P)\) qua \(O(0;0),A(80;60)\) và \(B(100;0)\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{c = 0}\\{{{80}^2}a + 80b = 60}\\{{{100}^2}a + 100b = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - \dfrac{3}{{80}}}\\{b = \dfrac{{15}}{4}}\end{array}} \right.} \right.\)
\( \Rightarrow (P):y = - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x\)
Bước 2: Tìm đỉnh của (P)
Vị trí đạn bay cao nhất cách mặt đất là \({y_I} = - \dfrac{\Delta }{{4a}} = - \dfrac{{{b^2} - 4ac}}{{4a}} = \dfrac{{375}}{4} = 93,75m\).
Hướng dẫn giải:
Bước 1: Đặt hệ trục tọa độ. Gọi \((P):y = a{x^2} + bx + c\). Tìm (P).
Bước 2: Tìm đỉnh của (P)
