Có bao nhiêu giá trị nguyên không âm của tham số m để hàm số $y = {x^4} - 2m{x^2} - 3m + 1$ đồng biến trên khoảng $(1;2)$?
Trả lời bởi giáo viên
$\begin{array}{*{20}{l}}{y = {x^4} - 2m{x^2} - 3m + 1 \Rightarrow y' = 4{x^3} - 4mx}\\{y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = m}\end{array}} \right.}\end{array}$
Theo đề bài, ta có: $m \ge 0$
+) Nếu $m = 0$ thì $y' = 4{x^3}$: Hàm số đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right) \supset (1;2){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Rightarrow m = 0$ thỏa mãn.
+) Nếu $m > 0$ thì $y' = 0$ có ba nghiệm phân biệt $x = 0,{\mkern 1mu} {\mkern 1mu} x = \pm \sqrt m $, hàm số đồng biến trên các khoảng $\left( { - \sqrt m ;0} \right),{\mkern 1mu} {\mkern 1mu} \left( {\sqrt m ; + \infty {\rm{\;}}} \right)$
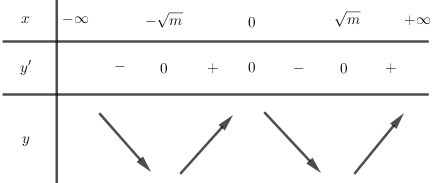
Để hàm số đồng biến trên khoảng $(1;2)$thì $\left[ \begin{array}{l}{\rm{\;}}(1;2) \subset \left( { - \sqrt m ;0} \right)\\{\rm{ \;}}(1;2) \subset {\mkern 1mu} \left( {\sqrt m ; + \infty {\rm{\;}}} \right)\end{array} \right.$
TH1: $(1;2) \subset \left( { - \sqrt m ;0} \right)$: Vô lí, do 2 > 0.
TH2: $(1;2) \subset {\mkern 1mu} \left( {\sqrt m ; + \infty {\rm{\;}}} \right) \Leftrightarrow \sqrt m \le 1 \Leftrightarrow m \le 1$
Vì $m > 0,{\mkern 1mu} {\mkern 1mu} m \in Z \Rightarrow m = 1$.
Vậy $m \in \left\{ {0;1} \right\}$, có 2 giá trị của m thỏa mãn yêu cầu đề bài.
Hướng dẫn giải:
Hàm số $y = f(x)$ đồng biến trên $D \Leftrightarrow f'(x) \ge 0,{\mkern 1mu} {\mkern 1mu} \forall x \in D$, $f'(x) = 0$ tại hữu hạn điểm thuộc D.
Giải thích thêm:
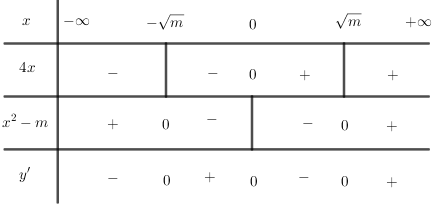
Các em tham khảo bảng xét dấu y' khi m > 0 như sau:
Cách khác:
$\begin{array}{l}
y' \ge 0,\forall x \in \left( {1;2} \right)\\
\Leftrightarrow 4{x^3} - 4mx \ge 0,\forall x \in \left( {1;2} \right)\\
\Leftrightarrow 4mx \le 4{x^3},\forall x \in \left( {1;2} \right)\\
\Leftrightarrow m \le {x^2},\forall x \in \left( {1;2} \right)
\end{array}$
Mà $1 < x < 2 \Rightarrow 1 < {x^2} < 4$ nên để $m \le {x^2},\forall x \in \left( {1;2} \right)$ thì $m \le 1$.
Câu hỏi khác
- Đề thi tư duy định lượng - Đề số 1 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 2 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 4 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 11 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 5 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
