Tìm các giá trị của tham số $m$ để phương trình ${x^2} - 2\left( {m + 1} \right)x + 1 = 0$ có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng $\left( {0;\,\,1} \right)$.
Trả lời bởi giáo viên
Có: \(\Delta ' = {\left( {m + 1} \right)^2} - 1 = m\left( {m + 2} \right)\)
Phương trình có hai nghiệm phân biệt \( \Leftrightarrow m\left( {m + 2} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}m > 0\\m < - 2\end{array} \right.\)
Khi đó dạng đồ thị hàm số \(y = {x^2} - 2\left( {m + 1} \right)x + 1\) chỉ có thể là:
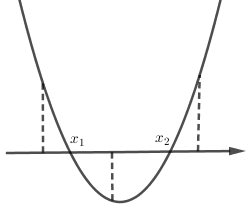
Quan sát đồ thị ta thấy:
Yêu cầu bài toán tương đương $f\left( 0 \right).f\left( 1 \right) < 0 \Leftrightarrow 1.\left( { - 2m} \right) < 0 \Leftrightarrow m > 0$
Kết hợp điều kiện có hai nghiệm phân biệt ta được $m>0$
Hướng dẫn giải:
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có đúng một nghiệm thuộc khoảng \(\left( {0;1} \right) \Leftrightarrow f\left( 0 \right).f\left( 1 \right) < 0\).
Giải thích thêm:
Điều kiện $f\left( a \right).f\left( b \right) < 0$ thì phương trình có một nghiệm duy nhất trong khoảng \(\left( {a;b} \right)\) chỉ đúng với trường hợp đặc biệt là phương trình bậc hai, còn nói chung điều đó chưa chắc đúng nên các em cần chú ý khi sử dụng điều kiện này.