Câu hỏi:
2 năm trước
Có bao nhiêu giá trị $m$ nguyên âm để mọi $x > 0$ đều thoả bất phương trình ${\left( {{x^2} + x + m} \right)^2} \ge {\left( {{x^2} - 3x - m} \right)^2}$?
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có ${\left( {{x^2} + x + m} \right)^2} \ge {\left( {{x^2} - 3x - m} \right)^2} \Leftrightarrow {\left( {{x^2} + x + m} \right)^2} - {\left( {{x^2} - 3x - m} \right)^2} \ge 0$
$ \Leftrightarrow 4x\left( {2x + m} \right)\left( {x - 1} \right) \ge 0$
Với \(m < 0\) ta có bảng xét dấu
TH1: \( - \dfrac{m}{2} \ge 1\)
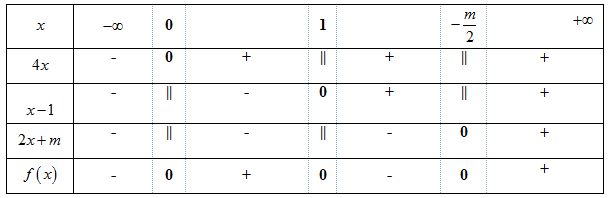
Từ Bảng xét dấu ta thấy để BPT nghiệm đúng với \(x > 0\) thì \( - \dfrac{m}{2} = 1 \Leftrightarrow m = - 2\)
TH 2: \(0< - \dfrac{m}{2} < 1\)
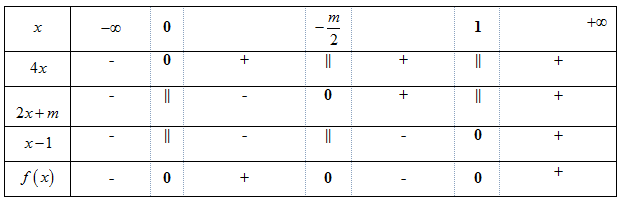
Từ Bảng xét dấu ta thấy để BPT nghiệm đúng với \(x > 0\) thì \( - \dfrac{m}{2} = 1 \Leftrightarrow m = - 2\)
Vậy có 1 giá trị
Hướng dẫn giải:
- Biến đổi bất phương trình về dạng tích.
- Chia thành các trường hợp để xét dấu vế trái của bất phương trình.
