Trả lời bởi giáo viên
Đáp án đúng: b
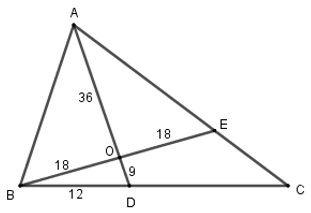
Ta có: \dfrac{{AO}}{{BO}} = \dfrac{{36}}{{18}} = 2, \dfrac{{OE}}{{OD}} = \dfrac{{18}}{9} = 2 nên \dfrac{{OA}}{{OB}} = \dfrac{{OE}}{{OD}} = 2
Xét \Delta AOE và \Delta BOD có:
\widehat {AOE} = \widehat {BOD} (đối đỉnh)
\dfrac{{OA}}{{OB}} = \dfrac{{OE}}{{OD}}\left( {cmt} \right)
\Rightarrow \Delta AOE \backsim \Delta BOD\left( {c.g.c} \right) nên A sai, B đúng.
Ngoài ra, \dfrac{{AO}}{{BO}} = \dfrac{{AE}}{{BD}} \Rightarrow \dfrac{{36}}{{18}} = \dfrac{{AE}}{{12}} \Rightarrow AE = \dfrac{{36.12}}{{18}} = 24 nên C, D sai.
Hướng dẫn giải:
Chứng minh tam giác đồng dạng theo trường hợp cạnh-góc-cạnh và sử dụng tính chất tam giác đồng dạng tính AE.

