Chọn khẳng định sai:

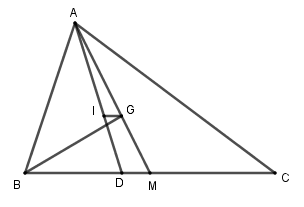
Gọi \(D, M\) là giao điểm của \(AI, AG\) với \(BC\).

Vì \(AD\) là tia phân giác góc \(\widehat {BAC}\) nên \(\dfrac{{BD}}{{AB}} = \dfrac{{DC}}{{AC}}\left( {t/c} \right)\)

\( \Rightarrow \dfrac{{BD}}{{12}} = \dfrac{{DC}}{{18}} = \dfrac{{BD + DC}}{{12 + 18}} = \dfrac{{15}}{{30}} = \dfrac{1}{2}\)

\( \Rightarrow BD = 12.\dfrac{1}{2} = 6, DC = 18.\dfrac{1}{2} = 9\)

Lại có: \(BI\) là tia phân giác góc \(\widehat {ABD}\) nên \(\dfrac{{AI}}{{ID}} = \dfrac{{AB}}{{BD}} = \dfrac{{12}}{6} = 2\) (tính chất)

\( \Rightarrow \dfrac{{ID}}{{AD}} = \dfrac{{MG}}{{MA}} = \dfrac{1}{3}\) hay D đúng.

Mà \(AG = 2GM\) (vì \(G\) là trọng tâm)

Nên \(\dfrac{{AI}}{{ID}} = \dfrac{{AG}}{{GM}} = 2\) hay B đúng.

Theo định lí đảo của định lí Ta-let ta có: \(IG//DM \Rightarrow IG//BC\) hay A đúng.

Chỉ có C sai.