Trả lời bởi giáo viên
Đáp án đúng: a
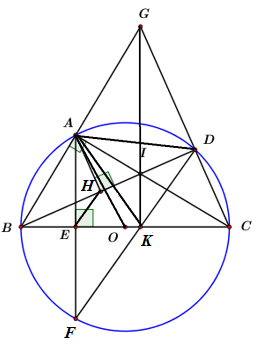
Xét ΔBHE và ΔBCI có:
Ta có: BC⊥AF⇒cungAB=cungFB (đường kính vuông góc với một dây thì đi qua điểm ở chính giữa của cung căng dây đó).
⇒∠BDF=∠BCA (hai góc nội tiếp chắn 2 cung bằng nhau).
Hay ∠IDK=∠ICK
⇒CDJK là tức giác nội tiếp. (tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau)
⇒∠IKC+∠IDC=1800. Mà ∠IDC=∠BDC=900(cmt)
⇒∠IKC=900⇒IK⊥BC(1)
Xét ΔGBC có {AC⊥BGBD⊥CGAC∩BD={I}
⇒I là trực tâm ΔGBC ⇒GI⊥BC(2)
Từ (1) và (2) ⇒G,I,K thằng hàng.
Hướng dẫn giải:
Chứng minh: IK⊥BC và GI⊥BC.

