Trả lời bởi giáo viên
Đáp án đúng: d
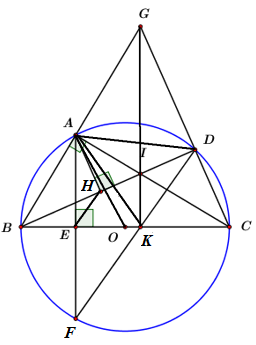
Xét tứ giác \(ABEH\) ta có: \(\angle AEB = \angle AHB = {90^0}\,\,\,\left( {gt} \right)\)
\( \Rightarrow ABEH\) là tứ giác nội tiếp. (tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau)
\( \Rightarrow \angle BHE = \angle BAE\) (hai góc nội tiếp cùng chắn cung \(BE\))
Mà \(\angle BAE = \angle BCA\) (hai góc cùng phụ \(\angle ABC\))
\( \Rightarrow \angle BHE = \angle BCA = \angle BCI\)
Xét \(\Delta BHE\) và \(\Delta BCI\) có:
\(\angle IBC\,\) chung
\(\angle BHE = \angle BCI\,\,\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{BE}}{{BI}} = \dfrac{{BH}}{{BC}} \Rightarrow BE.BC = BH.BI\,\)
Hướng dẫn giải:
Chứng minh: \(\angle BHE = \angle BCI\)
Câu hỏi khác
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Thành phố Hà Nội (Năm học 2021 - 2022) - có lời giải chi tiết
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Tỉnh Hải Dương (2021 - 2022) có lời giải chi tiết
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Tỉnh Thái Bình (2021 - 2022) có lời giải chi tiết
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT TP Đà Nẵng (2021 - 2022) có lời giải chi tiết
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Tỉnh Bình Dương (2021 - 2022) có lời giải chi tiết
