Trả lời bởi giáo viên
Đáp án đúng: b
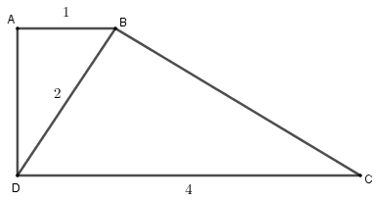
\Delta ABD và \Delta BDC có: \widehat {ABD} = \widehat {BDC} (hai góc ở vị trí so le trong bằng nhau doAB{\rm{//CD}});
Và \dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}} (vì \dfrac{1}{2} = \dfrac{2}{4}).
Do đó \Delta ABD \backsim \Delta BDC (c.g.c) nên A đúng.
\Rightarrow \widehat {ABD} = \widehat {BDC} < {90^0} nên B sai.
\Delta ABD \backsim \Delta BDC \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{1}{2} (cạnh t/u) \Leftrightarrow BC = 2AD nên C đúng.
\widehat {BAD} = \widehat {DBC} = {90^0} nên BD \bot BC hay D đúng.
Vậy chỉ có B sai.
Hướng dẫn giải:
- Xét tỉ số độ dài của các cạnh tương ứng của 2 tam giác.
- Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
