Trả lời bởi giáo viên
Đáp án đúng: b
Hàm số \(y = {x^\alpha }\left( {\alpha \ne 0} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\) nếu \(\alpha > 0\) nên A và C sai.
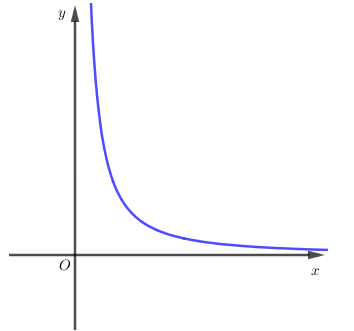
Hàm số \(y = {x^\alpha }\left( {\alpha \ne 0} \right)\) nghịch biến trên \(\left( {0; + \infty } \right)\) nếu \(\alpha < 0\) nên B đúng, D sai.
Hướng dẫn giải:
Sử dụng tính chất đơn điệu của hàm số \(y = {x^\alpha }\left( {\alpha \ne 0} \right)\) trên tạp khảo sát \(\left( {0; + \infty } \right)\).
Giải thích thêm:
Nhiều HS sẽ chọn đáp án C vì nghĩ hàm số luôn đồng biến là sai.
Một số em khác sẽ chọn đáp án D vì nhầm với tính đơn điệu của hàm số mũ là sai.
Nếu các em không nhớ điều kiện đồng biến nghịch biến thì cũng có thể xét tính đơn điệu của hàm số $y=x^\alpha $ bằng cách tính đạo hàm $y'$ rồi xét dấu của đạo hàm.
