Câu hỏi:
2 năm trước
Cho \(\widehat {xOA}\) và \(\widehat {yOA}\) là hai góc kề bù. Tia \(Oz,Ot\) lần lượt là hai tia phân giác của \(\widehat {xOA},\widehat {yOA}.\)
Tính \(\widehat {zOt}.\)
Trả lời bởi giáo viên
Đáp án đúng: b
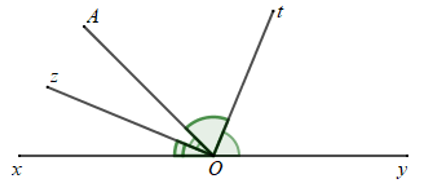
Ta có: \(\widehat {xOA} + \widehat {yOA} = 180^\circ \) (tính chất hai góc kề bù)
Vì \(Oz\) là phân giác \(\widehat {xOA}\) nên \(\widehat {xOz} = \widehat {zOA} = \dfrac{{\widehat {xOA}}}{2}\,\,\,\left( {\,1\,} \right)\)
Vì \(Ot\) là phân giác \(\widehat {yOA}\) nên \(\widehat {AOt} = \widehat {yOt} = \dfrac{{\widehat {yOA}}}{2}\,\,\,\left( {\,2} \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {zOA} + \widehat {AOt} = \dfrac{{\widehat {xOA}}}{2} + \dfrac{{\widehat {yOA}}}{2}\) \( = \dfrac{{\widehat {xOA} + \widehat {yOA}}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ \).
Hay \(\widehat {zOt} = 90^\circ \).
Hướng dẫn giải:
Áp dụng tính chất hai góc kề bù và tính chất tia phân giác của một góc.
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
