Cho tứ diện \(OABC\) có \(OA,{\rm{ }}OB,{\rm{ }}OC\) đôi một vuông góc với nhau. Gọi \(H\) là hình chiếu của \(O\) trên mặt phẳng \(\left( {ABC} \right)\). Mệnh đề nào sau đây là sai?
Trả lời bởi giáo viên
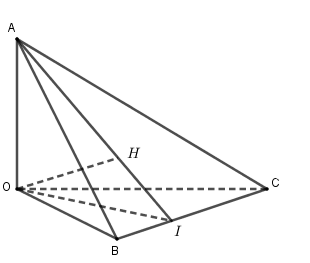
+) \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right. \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC.\) Do đó A đúng.
+) Do \(OH \bot \left( {ABC} \right)\) nên \(OH \bot AB\) nên B đúng.
Gọi \(I = AH \cap BC.\)
Theo giả thiết ta có $OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC.$ Suy ra \(BC \bot \left( {AOI} \right)\) \( \Rightarrow BC \bot OI,BC \bot AI\)
Gọi \(J = BH \cap AC.\) Chứng minh tương tự ta có \(AC \bot BJ\).
Suy ra $H$ là trực tâm \(\Delta ABC.\) Do đó C đúng.
Vậy D là đáp án sai vì \(AO \bot \left( {OBC} \right)\) và \(AO \ne AH\).
Hướng dẫn giải:
Xét tính đúng sai của từng đáp án, sử dụng lý thuyết đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng thuộc mặt phẳng và ngược lại.

