Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) có \(AC = \dfrac{3}{2}AD\), \(\widehat {CAB} = \widehat {DAB} = 60^\circ \), \(CD = AD\). Gọi \(\varphi \) là góc giữa \(AB\) và \(CD\). Chọn khẳng định đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
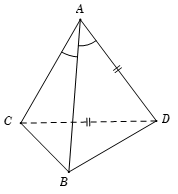
Ta có \(\cos \left( {AB,CD} \right) = \dfrac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}} = \dfrac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{AB.CD}}\)
Mặt khác \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \)
\(\begin{array}{l} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AD} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)\\ = AB.AD.\cos 60^\circ - AB.AC.\cos 60^\circ \\ = AB.AD.\dfrac{1}{2} - AB.\dfrac{3}{2}AD.\dfrac{1}{2} = - \dfrac{1}{4}AB.AD = - \dfrac{1}{4}AB.CD.\end{array}\)
Do có \(\cos \left( {AB,CD} \right) = \dfrac{{\left| { - \dfrac{1}{4}AB.CD} \right|}}{{AB.CD}} = \dfrac{1}{4}\).
Vậy \(\cos \varphi = \dfrac{1}{4}\).
Hướng dẫn giải:
Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CD} \) rồi sử dụng công thức \(\cos \left( {AB,CD} \right) = \dfrac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}}\).
