Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) có \(AB = AC = AD\) và \(\widehat {BAC} = \widehat {BAD} = 60^\circ \). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \)?
Trả lời bởi giáo viên
Đáp án đúng: d
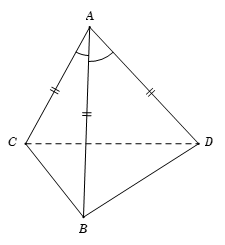
Ta có \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \)
\(\begin{array}{l} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AD} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)\\ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos 60^\circ - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos 60^\circ .\end{array}\)
Mà \(AC = AD \Rightarrow \overrightarrow {AB} .\overrightarrow {CD} = 0\)\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = 90^\circ \).
Hướng dẫn giải:
Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CD} \) và kết luận đáp án đúng.
