Câu hỏi:
2 năm trước
Cho tứ diện $ABCD$ có $AB$ vuông góc với $CD$. Mặt phẳng $\left( P \right)$ song song với $AB$ và $CD$ lần lượt cắt $BC,{\rm{ }}DB,{\rm{ }}AD,{\rm{ }}AC$ tại $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$. Tứ giác $MNPQ$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: c
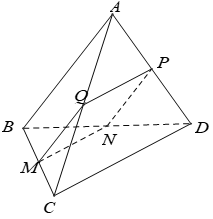
Ta có: $\left\{ \begin{array}{l}\left( {MNPQ} \right){\rm{//}}AB\\\left( {MNPQ} \right) \cap \left( {ABC} \right) = MQ\end{array} \right. $ $\Rightarrow MQ{\rm{//}}AB$
Tương tự ta có: \(MN{\rm{//}}CD,\,\,NP{\rm{//}}AB,\,\,QP{\rm{//}}C{\rm{D}}\).
Do đó tứ giác \(MNPQ\) là hình bình hành
lại có \(MN \bot MQ\left( {do\,AB \bot CD\,} \right)\).
Vậy tứ giác \(MNPQ\) là hình chữ nhật.
Hướng dẫn giải:
- Xác đinh thiết diện của hình tứ diện khi cắt bởi mặt phẳng \(\left( P \right)\).
- Xác định góc giữa hai đường thẳng \(MN,MQ\) bằng cách sử dụng tính chất \(\left\{ \begin{array}{l}a//a'\\b//b'\end{array} \right. \Rightarrow \widehat {\left( {a,b} \right)} = \widehat {\left( {a',b'} \right)}\)
