Cho tứ diện $ABCD$ có $AB$ vuông góc với $CD$, $AB = 4{,^{}}CD = 6$. $M$ là điểm thuộc cạnh $BC$ sao cho $MC = \dfrac{1}{2}BM$. Mặt phẳng $\left( P \right)$ đi qua $M$ song song với $AB$ và $CD$. Diện tích thiết diện của $\left( P \right)$ với tứ diện là:
Trả lời bởi giáo viên
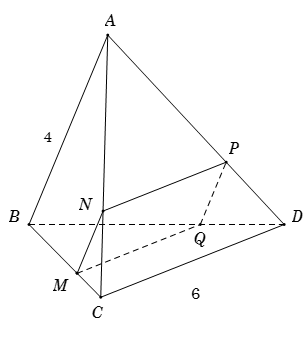
Ta có $\left\{ \begin{array}{l}\left( {MNPQ} \right){\rm{//}}AB\\\left( {MNPQ} \right) \cap \left( {ABC} \right) = MN\end{array} \right. \Rightarrow MN{\rm{//}}AB.$
Tương tự ta có \(MQ{\rm{//}}CD,\,\,NP{\rm{//}}CD,\,\,QP{\rm{//}}AB\). Do đó tứ giác \(MNPQ\) là hình bình hành
Ta có \(\left( {\widehat {AB;CD}} \right) = \left( {\widehat {MN;MQ}} \right) = \widehat {NMQ} = {90^0}\)\( \Rightarrow \) tứ giác \(MNPQ\) là hình chữ nhật.
Lại có $\Delta CMN\backsim \Delta CBA\Rightarrow \dfrac{CM}{CB}=\dfrac{MN}{AB}=\dfrac{1}{3}\Rightarrow MN=\dfrac{4}{3};$
$\Delta ANP\backsim \Delta ACD\Rightarrow \dfrac{AN}{AC}=\dfrac{NP}{CD}=\dfrac{2}{3}\Rightarrow NP=4.$
Vậy \({S_{MNPQ}} = MN.NP = \dfrac{{16}}{3}.\)
Hướng dẫn giải:
- Xác định thiết diện.
- Nhận xét tính chất thiết diện và tính diện tích.

