Câu hỏi:
3 năm trước
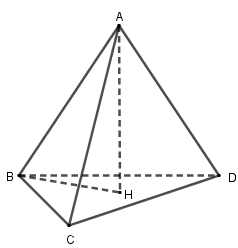
Cho tứ diện \(ABCD\) có \(AB \bot CD\) và \(AC \bot BD\). Gọi \(H\) là hình chiếu vuông góc của \(A\) lên \(mp(BCD)\). Chọn khẳng định đúng :
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có \(\left\{ \begin{array}{l}CD \bot AB\\CD \bot AH\end{array} \right. \Rightarrow CD \bot (ABH) \Rightarrow CD \bot BH\). Tương tự \(BD \bot CH\)
Suy ra \(H\) là trực tâm \(\Delta BCD\). Suy ra đáp án A, B, D sai.
Ta có \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot DH\end{array} \right. \Rightarrow BC \bot AD\), suy ra C đúng.
\( \to \) Chọn đáp án C.