Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) có \(AB = CD = a,IJ = \dfrac{{a\sqrt 3 }}{2}\) (\(I\), \(J\) lần lượt là trung điểm của \(BC\) và \(AD\)). Số đo góc giữa hai đường thẳng \(AB\) và \(CD\) là
Trả lời bởi giáo viên
Đáp án đúng: c
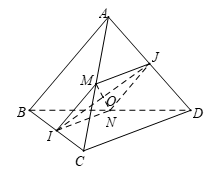
Gọi \(M\), \(N\) lần lượt là trung điểm \(AC\), \(BD.\)
Ta có:
\(\left\{ \begin{array}{l}MI = NI = \dfrac{1}{2}AB = \dfrac{1}{2}CD = \dfrac{a}{2}\\MI{\text{ // }}AB{\text{ // }}NJ,MJ//CD//IN\end{array} \right. \Rightarrow MINJ\) là hình thoi.
Gọi \(O\) là giao điểm của \(MN\) và \(IJ\).
Ta có: \(\widehat {MIN} = 2\widehat {MIO}\).
Xét \(\Delta MIO\) vuông tại \(O\), ta có: \(\cos \widehat {MIO} = \dfrac{{IO}}{{MI}} = \dfrac{{\dfrac{{a\sqrt 3 }}{4}}}{{\dfrac{a}{2}}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {MIO} = 30^\circ \Rightarrow \widehat {MIN} = 60^\circ \)
Mà: \(\left( {AB,CD} \right) = \left( {IM,IN} \right) = \widehat {MIN} = 60^\circ \)
Hướng dẫn giải:
Sử dụng tính chất: \(\left\{ \begin{array}{l}a//a'\\b//b'\end{array} \right. \Rightarrow \widehat {\left( {a,b} \right)} = \widehat {\left( {a',b'} \right)}\)
Giải thích thêm:
Các em cũng có thể tính $\widehat {JIN}$ bằng cách áp dụng định lý Cô sin trong tam giác JIN như sau:
$\cos \widehat {JIN} = \frac{{I{J^2} + I{N^2} - J{N^2}}}{{2IJ.IN}} $
$= \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}}}{{2.\frac{{a\sqrt 3 }}{2}.\frac{a}{2}}}$
$= \frac{{\sqrt 3 }}{2} $
$\Rightarrow \widehat {JIN} = {30^0}$
