Câu hỏi:
2 năm trước
Cho tam giác nhọn ABC có ˆC=400. Vẽ hình bình hành ABCD . Gọi AH,AK theo thứ tự là các đường cao của các tam giác ABC,ACD . Tính số đo ^AKH .
Trả lời bởi giáo viên
Đáp án đúng: b
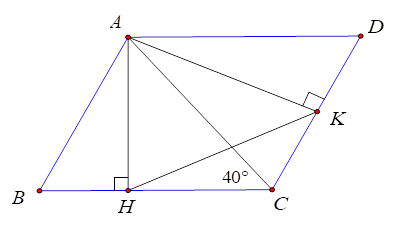
Vì AD.AH=AB.AK (=SABCD) nên AHAK=ABAD=ABBC.
Ta lại có AB//CD( vì ABCD là hình bình hành) mà AK⊥DC⇒AK⊥AB⇒^BAK=90∘.
Từ đó ^HAK=^ABC (cùng phụ với ^BAH )
Nên ΔAKH∽(c.g.c) \Rightarrow \widehat {AKH} = \widehat {ACB} = 40^\circ .
Hướng dẫn giải:
Bước 1: Sử dụng công thức diện tích hình bình hành để suy ra hệ thức về cạnh. Sử dụng quan hệ từ vuông góc đến song song và mối quan hệ giữa các góc để suy ra hai góc bằng nhau.
Bước 2: Từ đó suy ra \Delta AKH\backsim\Delta ACB và tính được \widehat {AKH} .