Câu hỏi:
2 năm trước
Cho tam giác ABC vuông tại A, có $\widehat B = {60^0}$và $AB{\rm{ }} = 5cm.$ Tia phân giác của góc $B$ cắt $AC$ tại $D.$ Kẻ $DE$ vuông góc với $BC$ tại $E.$
Tính độ dài cạnh $BC.$
Trả lời bởi giáo viên
Đáp án đúng: a
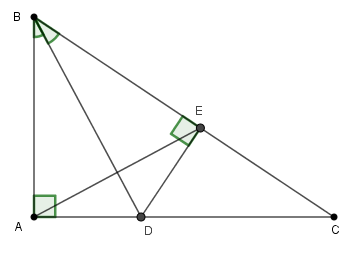
Ta có: $\widehat {EAC} + \widehat {BAE} = {90^0}$(gt)
$\widehat C + \widehat B = {90^0}$ (\(\Delta \)$ABC$ vuông tại A)
Mà $\widehat {BAE} = \widehat B = {60^0}$ ( do \(\Delta \)ABE đều) nên $\widehat {EAC} = \widehat C$
\( \Rightarrow \) \(\Delta \)AEC cân tại E
\( \Rightarrow EA = EC\) mà $EA = AB = EB = 5cm$
Do đó $EC = 5cm$
Vậy $BC = EB + EC = 5cm + 5cm = 10cm.$
Hướng dẫn giải:
+ Ta đi chứng minh tam giác $AEC$ cân tại $E$ vì có hai góc ở đáy bằng nhau; từ đó suy ra hai cạnh bên bằng nhau để tính được độ dài cạnh $EC$ ; tính $BC$ bằng cách \(BC = BE + EC\).
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
