Câu hỏi:
2 năm trước
Cho tam giác ABC vuông tại A, có $\widehat B = {60^0}$và $AB{\rm{ }} = 5cm.$ Tia phân giác của góc $B$ cắt $AC$ tại $D.$ Kẻ $DE$ vuông góc với $BC$ tại $E.$
Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: b
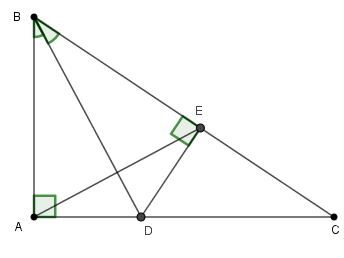
Xét $\Delta ABD$ và \(\Delta \)$EBD$ , có:
+ $\widehat {BAD} = \widehat {BED} = {90^0}(gt)$
+ BD là cạnh huyền chung
+ $\widehat {ABD} = \widehat {EBD}(gt)$
Vậy \(\Delta ABE = \Delta EBD\) (cạnh huyền – góc nhọn) nên A sai.
Ta có: \(\Delta ABE = \Delta EBD\)(cmt)\( \Rightarrow AB = EB \) (hai cạnh tương ứng).
Do đó \(\Delta \)ABE cân tại B.
Mà \(\widehat B = {60^0}\) (gt) nên \(\Delta ABE\) đều. (dhnb)
Hướng dẫn giải:
+ Sử dụng trường hợp bằng nhau cạnh huyền – góc nhọn để chứng minh hai tam giác vuông bằng nhau
+ Từ cặp tam giác bằng nhau trên ta suy ra hai cạnh tương ứng bằng nhau, từ đó lập luận để suy ra tính chất của tam giác \(ABE.\)
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
