Cho tam giác $ABC$ và $H$ là trực tâm. Các đường thẳng vuông góc với $AB$ tại $B$ , vuông góc với $AC$ tại $C$ cắt nhau ở $ D$ .
Tính số đo góc \(BDC\) , biết $\widehat {BAC} = 50^\circ $.
Trả lời bởi giáo viên
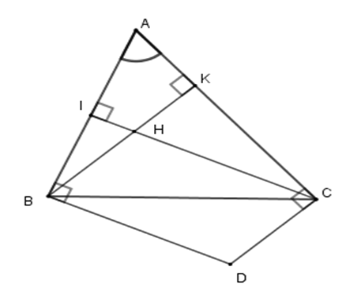
Xét tứ giác \(AIHK\) có \(\widehat A + \widehat {AIH} + \widehat {IHK} + \widehat {AKH} = 360^\circ \) (định lý tổng các góc trong tứ giác)
\( \Rightarrow \widehat {AHK} = 360^\circ - 50^\circ - 90^\circ - 90^\circ = 130^\circ \) .
Suy ra \(\widehat {BHC} = \widehat {IHK} = 130^\circ \) (hai góc đối đỉnh)
Vì tứ giác \(BHCD\) là hình bình hành nên $\widehat {BDC} = \widehat {BHC} = 130^\circ $ (tính chất).
Vậy \(\widehat {BDC} = 130^\circ \) .
Hướng dẫn giải:
Bước 1: Sử dụng định lý tổng các góc trong tứ giác để tính góc \(IHK\) .
Bước 2: Sử dụng tính chất của hình bình hành để tính góc \(BDC\) .

