Câu hỏi:
2 năm trước
Cho tam giác $ABC$ và $H$ là trực tâm. Các đường thẳng vuông góc với $AB$ tại $B$ , vuông góc với $AC$ tại $C$ cắt nhau ở $ D$ .
Chọn câu trả lời đúng nhất. Tứ giác $BDCH$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: b
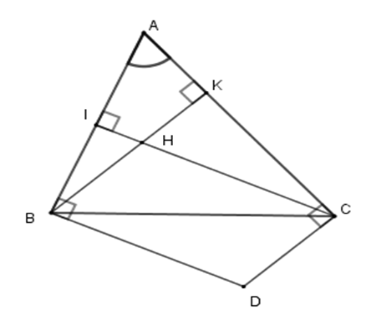
Gọi \(BK;\,CI\) là các đường cao của tam giác \(ABC\) . Khi đó \(BK \bot AC;\,CI \bot AB\) hay \(BH \bot AC;\,CH \bot AB\) (vì \(H\) là trực tâm).
Lại có \(BD \bot AB;\,CD \bot AC\) (giả thiết) nên $BD{\rm{//}}CH$ (cùng vuông với \(AB\) ) và $CD{\rm{//}}BH$ (cùng vuông với \(AC\) )
Suy ra tứ giác \(BHCD\) là hình bình hành (dhnb).
Hướng dẫn giải:
Bước 1: Sử dụng quan hệ từ vuông góc đến song song để chứng minh các cặp cạnh song song.
Bước 2: Sử dụng dấu hiệu nhận biết của hình bình hành để suy ra $BDCH$ là hình bình hành

