Cho tam giác \(ABC\) nhọn có trực tâm \(H.\) Chọn câu đúng.

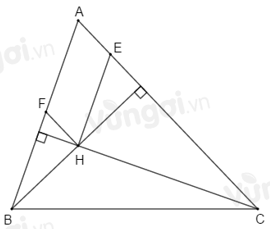
Qua \(H\) kẻ đường thẳng song song với \(AC\) cắt \(AB\) tại \(F\), kẻ đường thẳng song song với \(AB\) cắt \(AC\) tại \(E\).

Vì \(AE//HF\) (cách vẽ) nên \(\widehat {EAH} = \widehat {FHA}\) (hai góc so le trong bằng nhau)

Vì \(AF//HE\) (cách vẽ) nên \(\widehat {AHE} = \widehat {HAF}\) (hai góc so le trong bằng nhau)

Xét \(\Delta AEH\) và \(\Delta HFA\) có:

\(AH\) cạnh chung

\(\widehat {EAH} = \widehat {FHA}\,\,(cmt)\)

\(\widehat {AHE} = \widehat {HAF}\,\,(cmt)\)

\( \Rightarrow \Delta AEH = \Delta HFA\,(g.c.g)\)

\( \Rightarrow EH = AF;\,AE = HF\) (hai cạnh tương ứng).

Vì \(BH \bot AC\) và \(FH//AC\) nên \(BH \bot FH\).

Ta có: \(BF;\,BH\) lần lượt là đường xiên và đường vuông góc kẻ từ \(B\) đến \(FH\) nên \(BF > BH\) (quan hệ đường xiên – đường vuông góc).

Vì \(CH \bot AB\) và \(EH//AB\) nên \(CH \bot EH\).

Ta có: \(CE;\,CH\) lần lượt là đường xiên và đường vuông góc kẻ từ \(C\) đến \(EH\) nên \(CE > CH\) (quan hệ đường xiên – đường vuông góc).

Xét \(\Delta AEH\) có: \(AE + EH > HA\) (bất đẳng thức tam giác)

Ta có: \(AB + AC = AF + FB + AE + EC\)

\( \Rightarrow AB + AC = EH + FB + AE + EC\) (vì \(AF = EH\,(cmt)\))

\( \Rightarrow AB + AC = \left( {AE + EH} \right) + FB + EC > HA + HB + HC\).

Vậy \(AB + AC > HA + HB + HC\).