Cho tam giác \(ABC\) có \(BC = 6cm.\) Trên cạnh \(AB\) lấy các điểm \(D\) và \(E\) sao cho \(AD = BE.\) Qua \(D,E\) lần lượt vẽ các đường thẳng song song với \(BC,\) cắt \(AC\) theo thứ tự ở \(G\) và \(H\). Tính tổng \(DG + EH.\)

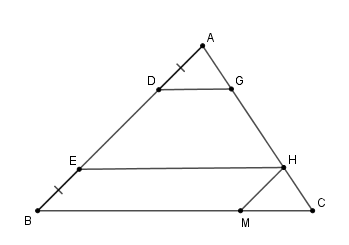
Kẻ \(HM//AB\,\,\left( {M \in BC} \right)\).

Xét tứ giác \(EHMB\) có \(MH//EB;EH//BM\) nên \(EHMB\) là hình bình hành.

Suy ra \(EH = BM;\,EB = HM\) (tính chất hình bình hành) mà \(AD = BE \Rightarrow AD = MH\).

Lại có: \(DG//BC \Rightarrow \widehat {ADG} = \widehat {ABC}\) (hai góc ở vị trí đồng vị) (1)

Và \(HM//AB \Rightarrow \widehat {HMC} = \widehat {ABC}\) và \(\widehat {CHM} = \widehat {CAB}\) (hai góc ở vị trí đồng vị) (2)

Từ (1) và (2) suy ra: \(\widehat {HMC} = \widehat {ADG}\left( { = \widehat {ABC}} \right)\).

Xét \(\Delta ADG\) và \(\Delta HMC\) có: \(\left\{ \begin{array}{l}\widehat {MHC} = \widehat {DAG}\left( {cmt} \right)\\AD = HM\,\left( {cmt} \right)\\\widehat {HMC} = \widehat {ADG}\left( {cmt} \right)\end{array} \right.\) nên \(\Delta ADG = \Delta HMC\left( {g - c - g} \right) \Rightarrow DG = MC\).

Ta có: \(DG + EH = MC + BM = BC = 6cm\).