Cho tam giác \(ABC\) có \(\angle B,\angle C\) là góc nhọn và có diện tích không đổi. Tìm giá trị nhỏ nhất của biểu thức \(P = 2B{C^2} + A{C^2} + A{B^2}\).
Trả lời bởi giáo viên
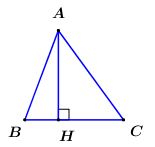
Kẻ đường cao \(AH\). Vì \(\angle B,\,\,\angle C\) là các góc nhọn nên \(H\) thuộc đoạn thẳng \(BC\).
Áp dụng định lí Pytago ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\A{B^2} = A{H^2} + B{H^2}\end{array}\)
\( \Rightarrow P = 2B{C^2} + 2A{H^2} + B{H^2} + H{C^2}\).
Ta có \(B{C^2} + A{H^2} \ge 2BC.AH = 4{S_{\Delta ABC}}\).
\(B{H^2} + C{H^2} \ge \dfrac{{{{\left( {BH + CH} \right)}^2}}}{2} = \dfrac{{B{C^2}}}{2}\).
Do đó \(P \ge 8{S_{\Delta ABC}} + \dfrac{{B{C^2}}}{2}\).
Do \({S_{\Delta ABC}}\) không đổi, \(A,\,\,B,\,\,C\) cố định nên \(P\) đạt giá trị nhỏ nhất bằng \(8{S_{\Delta ABC}} + \dfrac{{B{C^2}}}{2}\).
Dấu “=” xảy ra khi \(BH = CH \Rightarrow \Delta ABC\) cân tại \(A\).
Hướng dẫn giải:
Kẻ đường cao \(AH\) của tam giác \(ABC\)
Áp dụng định lí Py – ta – go, tính được \(P = \left( {B{C^2} + A{H^2}} \right) + \left( {B{H^2} + C{H^2}} \right)\)
Áp dụng các bất đẳng thức, tìm được giá trị nhỏ nhất của \(P\).

