Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có $AB = AC = 10cm,{\rm{ }}BC = 12cm.$ Vẽ $AH$ vuông góc $BC$ tại $H.$ Từ H vẽ $HM \bot AB$\((M \in AB)\) và vẽ $HN$ \( \bot \)$AC$ \((N \in AC)\). Đường thẳng vuông góc với \(AB\) tại \(B\) và đường thẳng vuông góc với \(AC\) tại \(C\) cắt nhau tại \(O.\)
Tam giác \(OBC\) là tam giác
Trả lời bởi giáo viên
Đáp án đúng: a
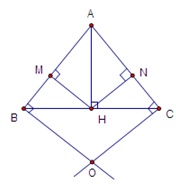
+) Ta có: \(\widehat {CBO} = {90^0} - \widehat {ABC}\) (hai góc phụ nhau)
\(\widehat {BCO} = {90^0} - \widehat {ACB}\) (hai góc phụ nhau)
Mà \(\widehat {ABC} = \widehat {ACB}\) ($\Delta ABC\;$ cân tại $A$ )
Do đó: \(\widehat {CBO} = \widehat {BCO}\) nên $\Delta OBC$ cân tại $O$ (dhnb).
Hướng dẫn giải:
Chứng minh \(\widehat {CBO} = \widehat {BCO}\) để suy ra tính chất tam giác \(OBC.\)
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
