Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có $AB = AC = 10cm,{\rm{ }}BC = 12cm.$ Vẽ $AH$ vuông góc $BC$ tại $H.$ Từ H vẽ $HM \bot AB$\((M \in AB)\) và vẽ $HN$ \( \bot \)$AC$ \((N \in AC)\). Đường thẳng vuông góc với \(AB\) tại \(B\) và đường thẳng vuông góc với \(AC\) tại \(C\) cắt nhau tại \(O.\)
Tính \(AH.\)
Trả lời bởi giáo viên
Đáp án đúng: d
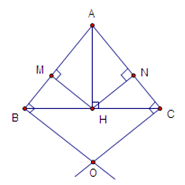
Vì tam giác \(ABC\) có \(AB = AC\) nên tam giác \(ABC\) cân tại \(A.\) Lại có \(AH\) là đường cao nên \(AH\) cũng là đường trung tuyến.
Ta có $BH = HC = $\(\dfrac{{BC}}{2} = \dfrac{{12}}{2} = 6\)cm
Xét \(\Delta AHB\) vuông tại $H,$ theo định lí Pytago ta có:
$\begin{array}{l}A{B^2} = A{H^2} + H{B^2} \Leftrightarrow {10^2} = A{H^2} + {6^2}\\ \Rightarrow A{H^2} = {10^2} - {6^2} \Leftrightarrow A{H^2} = 64\\ \Rightarrow AH = 8cm\end{array}$
Hướng dẫn giải:
Sử dụng định lí Py-ta-go trong \(\Delta AHB\) vuông tại $H$ để tính $AH.$
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
