Cho tam giác $ABC$  có $\widehat A = {50^0},\widehat B = {70^0}.$ Tia phân giác của góc C cắt cạnh AB tại M. Tính \(\widehat {AMC}\) và \(\widehat {BMC}.\)

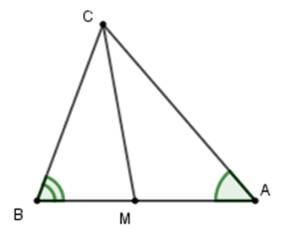
Xét tam giác \(ABC\) có \(\widehat A + \widehat B + \widehat {BCA} = 180^\circ \)(định lý tổng ba góc trong tam giác) mà $\widehat A = {50^0},\widehat B = {70^0}.$ Suy ra \(\widehat {BCA} = 180^\circ  - 50^\circ  - 70^\circ  = 60^\circ .\)

Vì \(CM\) là tia phân giác của góc \(BCA\) nên \(\widehat {BCM} = \widehat {ACM} = \dfrac{{\widehat {BCA}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ \)

Ta có \(\widehat {AMC}\) là góc ngoài tại đỉnh \(M\) của tam giác \(BCM\) nên ta có

\(\widehat {AMC} = \widehat B + \widehat {BCM} = 70^\circ  + 30^\circ  = 100^\circ \)

Lại có \(\widehat {AMC} + \widehat {BMC} = 180^\circ \) (hai góc kề bù) suy ra \(\widehat {BMC} = 180^\circ  - \widehat {AMC} = 80^\circ .\)

Vậy \(\widehat {AMC} = 100^\circ ;\,\widehat {BMC} = 80^\circ .\)