Câu hỏi:
3 năm trước
Cho tam giác \(ABC\) cân tại $A$ . Vẽ đường tròn tâm $O$, đường kính \(BC\). Đường tròn \(\left( O \right)\) cắt $AB$, $AC$ lần lượt tại \(I,K.\)
Tính $\widehat {IOK}$ biết $\widehat {BAC} = 40^\circ $
Trả lời bởi giáo viên
Đáp án đúng: b
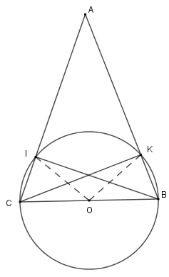
Xét tam giác $ABC$ cân tại $A$ có $\widehat A = 40^\circ \Rightarrow \widehat {KBO} = \widehat {ICO} = 70^\circ $
Xét tam giác $OKB$cân tại $O$ có $\widehat {KBO} = 70^\circ \Rightarrow \widehat {KOB} = 180^\circ - 2.70^\circ = 40^\circ $
Tương tự ta có $\widehat {IOC} = 40^\circ $
Suy ra $\widehat {IOK} = 180^\circ - 40^\circ - 40^\circ = 100^\circ $
Hướng dẫn giải:
Sử dụng tổng các góc trong tam giác

