Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) cân tại $A$ . Vẽ đường tròn tâm $O$, đường kính \(BC\). Đường tròn \(\left( O \right)\) cắt $AB$, $AC$ lần lượt tại \(I,K.\)
So sánh các cung nhỏ $BI$ và cung nhỏ $CK$
Trả lời bởi giáo viên
Đáp án đúng: a
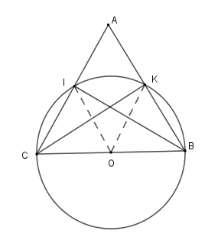
Xét các tam giác $\Delta IBC$ và .$\Delta KBC$ có $BC$ là đường kính của $\left( O \right)$ và $I;K \in \left( O \right)$
Nên $\Delta IBC$ vuông tại $I$ và $\Delta KBC$ vuông tại $K$
Xét hai tam giác vuông $\Delta IBC$ và .$\Delta KBC$ ta có $BC$ chung; $\widehat {ACB} = \widehat {ABC}$ (do$\Delta ABC$ cân)
$ \Rightarrow \Delta IBC = \Delta KCB\left( {ch - gn} \right) \Rightarrow IB = CK$
Suy ra $\Delta COK = \Delta IOB\left( {c - c - c} \right)$$ \Rightarrow \widehat {COK} = \widehat {IOB}$ suy ra số đo hai cung nhỏ $CK$ và $BI$ bằng nhau.
Hướng dẫn giải:
Sử dụng tam giác bằng nhau
So sánh hai cung
