Câu hỏi:
3 năm trước
Cho tam giác $ABC$, các đường trung tuyến $BD$ và $CE$ cắt nhau ở $G$. Gọi $I,K$ theo thứ tự là trung điểm của $GB,GC$. Trong các câu sau câu nào đúng?
Trả lời bởi giáo viên
Đáp án đúng: c
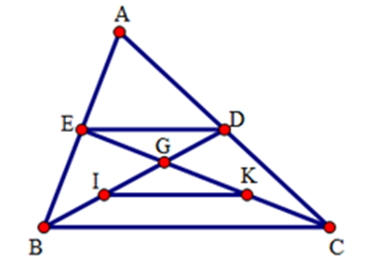
Vì tam giác $ABC$ có $AE = EB,AD = DC$ nên $ED$ là đường trung bình, do đó \(ED{\rm{//}}BC,ED = \dfrac{1}{2}BC\).
Tương tự tam giác $GBC$ có $GI = IB,GK = KC$ nên $IK$ là đường trung bình, do đó $IK{\rm{//}}BC,IK = \dfrac{1}{2}BC$.
Suy ra $ED{\rm{//}}IK$ (cùng song song với $BC$); $ED = IK$ (cùng bằng $\dfrac{1}{2}BC$).
Hướng dẫn giải:
Bước 1: Sử dụng dấu hiệu nhận biết để chứng minh các đường thẳng lần lượt là các đường trung bình của các tam giác tương ứng.
Bước 2: Sau đó sử dụng định lý của các đường trung bình để suy ra các mỗi liên hệ giữa các đoạn thẳng.

