Cho số phức ${z_1}$ thỏa mãn ${\left| {{z_1} - 2} \right|^2} - {\left| {{z_1} + i} \right|^2} = 1$ và số phức ${z_2}$ thỏa mãn $\left| {{z_2} - 4 - i} \right| = \sqrt 5$. Tìm giá trị nhỏ nhất của $P = \left| {{z_1} - {z_2}} \right|$.

Gọi $z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)$. Ta có

${{\left| z-2 \right|}^{2}}-{{\left| z+i \right|}^{2}}=1$ $\to {{\left( x-2 \right)}^{2}}+{{y}^{2}}-{{x}^{2}}-{{\left( y+1 \right)}^{2}}=1$ $\xrightarrow{{}}2x+y-1=0$.

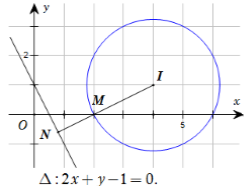
Suy ra tập hợp các số phức ${z_1}$ là đường thẳng $\Delta :2x + y - 1 = 0.$

$\left| z-4-i \right|=\sqrt{5}\xrightarrow{{}}\left| \left( x-4 \right)+\left( y-1 \right)i \right|=\sqrt{5}$

$\Leftrightarrow {{\left( x-4 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=5$

Suy ra tập hợp các số phức ${z_2}$ là đường tròn $\left( C \right):{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 5$ có tâm $I\left( {4;1} \right)$ và bán kính $R = \sqrt 5 .$

Khi đó biểu thức $P = \left| {{z_1} - {z_2}} \right|$ là khoảng cách từ một điểm thuộc $\Delta$ đến một điểm thuộc $\left( C \right)$.

Từ đó suy ra ${P_{\min }} = MN = \left| {d\left[ {I,\Delta } \right] - R} \right|$ $= \left| {\dfrac{8}{{\sqrt 5 }} - \sqrt 5 } \right| = \dfrac{{3\sqrt 5 }}{5}.$