Câu hỏi:
3 năm trước
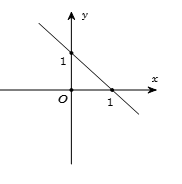
Tập hợp các điểm biểu diễn hình học của số phức $z$ là đường thẳng $\Delta $ như hình vẽ. Tìm giá trị nhỏ nhất của \(\left| z \right|\).
Trả lời bởi giáo viên
Đáp án đúng: d
\(\Delta \) đi qua hai điểm \(\left( {1;0} \right)\) và \(\left( {0;1} \right)\) nên có phương trình $\Delta :x + y - 1 = 0$.
Khi đó ${\left| z \right|_{\min }} = d\left[ {O,\Delta } \right] = \dfrac{{\left| { - 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{1}{{\sqrt 2 }}.$
Hướng dẫn giải:
- Viết phương trình \(\Delta \) suy ra khoảng cách theo công thức \(d\left( {A,\Delta } \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

