Câu hỏi:
2 năm trước
Cho phương trình \(2{x^4} - 5{x^2} + x + 1 = 0\,\,\,\left( 1 \right)\). Trong các mệnh đề sau, mệnh đề nào đúng?
Trả lời bởi giáo viên
Đáp án đúng: b
TXĐ: D = R. Hàm số \(f\left( x \right) = 2{x^4} - 5{x^2} + x + 1\) liên tục trên R.
Ta có: $f\left( { - 1} \right) = - 3,\,\,f\left( 0 \right) = 1 \Rightarrow f\left( { - 1} \right)f\left( 0 \right) < 0 \Rightarrow $ Phương trình (1) có ít nhất một nghiệm trong \(\left( { - 1;0} \right) \subset \left( { - 2;1} \right)\)
Ta có \(f\left( 0 \right) = 1;f\left( 1 \right) = - 1 \Rightarrow f\left( 0 \right).f\left( 1 \right) < 0 \Rightarrow \) Phương trình (1) có ít nhất 1 nghiệm thuộc $\left( {0;1} \right) \subset \left( { - 2;1} \right)$
\( \Rightarrow \) Phương trình (1) có ít nhất hai nghiệm trong \(\left( { - 2;1} \right) \Rightarrow \) Đáp án A sai.
Ta có: $f\left( { - 1} \right) = - 3,\,\,f\left( 0 \right) = 1 \Rightarrow f\left( { - 1} \right)f\left( 0 \right) < 0 \Rightarrow $ Phương trình (1) có ít nhất một nghiệm trong \(\left( { - 1;0} \right) \subset \left( { - 2;0} \right) \Rightarrow \)Đáp án C sai.
Ta có \(f\left( 0 \right) = 1;f\left( 1 \right) = - 1 \Rightarrow f\left( 0 \right).f\left( 1 \right) < 0 \Rightarrow \) Phương trình (1) có ít nhất 1 nghiệm thuộc $\left( {0;1} \right) \subset \left( { - 1;1} \right) \Rightarrow $ Đáp án D sai.
Hướng dẫn giải:
Hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {a;b} \right)\) và \(f\left( a \right).f\left( b \right) < 0\) thì tồn tại ít nhất một số \({x_0} \in \left( {a;b} \right)\) sao cho x0 là nghiệm của phương trình \(f\left( x \right) = 0\).
Giải thích thêm:
- Trong bài trên ở mỗi đáp án có các điểm đầu mút nên ta nghĩ đến đi tính giá trị hàm số tại các điểm đó.
- Trong trường hợp không có các khoảng cụ thể, các em dùng chức năng Table (MODE 7) ở máy tính cầm tay để lập bảng giá trị hàm số, từ đó tìm các x liên tiếp nhau mà f thay đổi đột ngột từ âm sang dương và từ dương sang âm.
- Đối với máy tính Fx580VN có thể bấm như sau:
Bấm phím MENU, ấn 8 = rồi nhập hàm \(f\left( x \right) = 2{x^4} - 5{x^2} + x + 1\)
Ấn = hiện ra g(x) thì không nhập và ấn = hiện ra giao diện như sau:
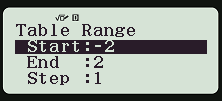
Ở đó, dòng Start nhập -2, ấn =
Dòng End nhập 2, ấn =
Dòng Step nhập 1, ấn =
Hiện ra bảng giá trị của hàm số và nhìn bên cột f(x) các giá trị thay đổi đột ngột từ âm sang dương và dương sang âm.
Ví dụ:
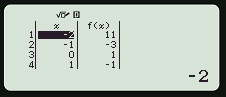
Nhận thấy, với \(x = - 2\) thì bên cột f(x) hiện 11 tức là \(f\left( { - 2} \right) = 11\)
Tương tự \(f\left( { - 1} \right) = - 3\) và dễ thấy \(f\left( { - 2} \right).f\left( { - 1} \right) < 0\) nên phương trình có ít nhất 1 nghiệm trong khoảng \(\left( { - 2; - 1} \right)\).
Câu hỏi khác
- Đề thi kiểm tra giữa học kì 1 - Đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 3 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 5 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 4 Toán 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 2 Toán 11 có lời giải chi tiết
