Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau. Gọi $H$ là hình chiếu của $O$ trên mặt phẳng $\left( {ABC} \right)$. Xét các mệnh đề sau :
I. Vì $OC \bot OA,OC \bot OB$ nên $OC \bot \left( {OAB} \right)$.
II. Do $AB \subset \left( {OAB} \right)$nên $AB \bot OC.{\rm{ }}\left( 1 \right)$
III. Có $OH \bot \left( {ABC} \right)$ và $AB \subset \left( {ABC} \right)$nên $AB \bot OH.{\rm{ }}\left( 2 \right)$
IV. Từ $\left( 1 \right)$ và $\left( 2 \right) \Rightarrow AB \bot \left( {OCH} \right)$
Số mệnh đề đúng trong các mệnh đề trên là:
Trả lời bởi giáo viên
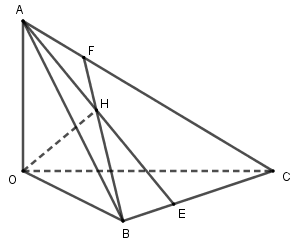 Ta có:
Ta có:
$\left\{ \begin{array}{l}OC \bot OA\\OC \bot OB\\OA \cap OB = O\\OA,OB \subset \left( {OAB} \right)\end{array} \right. \Rightarrow OC \bot \left( {OAB} \right)$.
Vậy $I$ đúng.
$\left\{ \begin{array}{l}OC \bot \left( {OAB} \right)\\AB \subset \left( {OAB} \right)\end{array} \right. \Rightarrow AB \bot OC$.
Vậy $II$ đúng.
$\left\{ \begin{array}{l}OH \bot \left( {ABC} \right)\\AB \subset \left( {ABC} \right)\end{array} \right. \Rightarrow AB \bot OH$.
Vậy $III$ đúng.
$\left\{ {\begin{array}{*{20}{c}}{AB \bot OC}\\{AB \bot OH}\\\begin{array}{l}OC \cap OH = O\\OC,OH \subset \left( {OCH} \right)\end{array}\end{array}} \right. \Rightarrow AB \bot \left( {OCH} \right)$.
Vậy $IV$ đúng.
Hướng dẫn giải:
Sử dụng điều kiện đường thẳng vuông góc mặt phẳng để xét tính đúng, sai cho từng mệnh đề.

