Câu hỏi:
2 năm trước
Cho nửa đường tròn $\left( O \right)$, đường kính $AB$. Vẽ nửa đường tròn tâm $O'$ đường kính $AO$ (cùng phía với nửa đường tròn $\left( O \right)$). Một cát tuyến bất kỳ qua $A$ cắt $\left( {O'} \right);\left( O \right)$ lần lượt tại $C,D$.
Nếu $BC$ là tiếp tuyến của nửa đường tròn $\left( {O'} \right)$ thì tính $BC$ theo $R$ (với $OA = R$)
Trả lời bởi giáo viên
Đáp án đúng: b
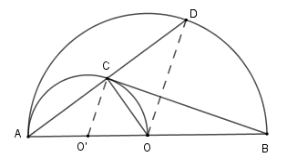
Ta có $OB = R;OO' = \dfrac{R}{2} \Rightarrow O'B = \dfrac{{3R}}{2}$;$O'C = \dfrac{R}{2}$
Theo định lý Pytago ta có $BC = \sqrt {O'{B^2} - O'{C^2}} = \sqrt {\dfrac{{9{R^2}}}{4} - \dfrac{{{R^2}}}{4}} = \sqrt 2 R$
Hướng dẫn giải:
Sử dụng định lý Pytago
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
