Câu hỏi:
2 năm trước
Cho nửa đường tròn $\left( O \right)$, đường kính $AB$. Vẽ nửa đường tròn tâm $O'$ đường kính $AO$ (cùng phía với nửa đường tròn $\left( O \right)$). Một cát tuyến bất kỳ qua $A$ cắt $\left( {O'} \right);\left( O \right)$ lần lượt tại $C,D$.
Chọn khẳng định sai?
Trả lời bởi giáo viên
Đáp án đúng: d
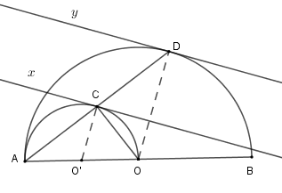
Xét đường tròn $\left( {O'} \right)$ có $AO$ là đường kính và $C \in \left( {O'} \right)$ nên $\widehat {ACO} = 90^\circ \Rightarrow AD \bot CO$
Xét đường tròn $\left( O \right)$ có $OA = OD \Rightarrow \Delta OAD$ cân tại $O$ có $OC$ là đường cao nên $OC$ cũng là đường trung tuyến hay $C$ là trung điểm của $AD$.
Xét tam giác $AOD$ có $O'C$ là đường trung bình nên $O'C{\rm{//}}OD$
Kẻ các tiếp tuyến $Cx;Dy$ với các nửa đường tròn ta có $Cx \bot O'C;Dy \bot OD$ mà $O'C{\rm{//}}OD$ nên $Cx{\rm{//}}Dy$
Do đó phương án A, B, C đúng.
Hướng dẫn giải:
Sử dụng đường trung bình của tam giác và quan hệ từ vuông góc đến song song
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
