Câu hỏi:
2 năm trước
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
Trả lời bởi giáo viên
Đáp án đúng: d
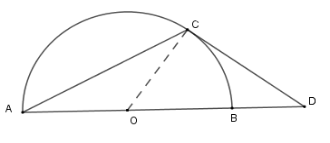
Xét nửa \(\left( O \right)\) có \(\widehat {BAC} = \dfrac{1}{2}\) sđ \(\overparen{BC}\) (góc nội tiếp chắn cung BC) và \(\widehat {CDA} = \dfrac{1}{2}\) (sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\) ) (góc có đỉnh bên ngoài đường tròn)
Mà \(\Delta ADC\) cân tại \(C\) nên \(\widehat {DAC} = \widehat {CDA} \Leftrightarrow \) sđ \(\overparen{BC} = \) sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\)
Suy ra sđ \(\overparen{AC} = 2\). sđ \(\overparen{BC}\)
Mà sđ \(\overparen{AC} + \) sđ \(\overparen{BC} = 180^\circ \) nên sđ \(\overparen{AC} = 120^\circ \) ; sđ\(\overparen{BC}= 60^\circ \)
Do đó $\widehat {ADC} = 30^\circ $.
Hướng dẫn giải:
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
Câu hỏi khác
Câu 6:
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |
139
