Câu hỏi:
3 năm trước
Cho một hình quạt tròn có bán kính \(20\,cm\) và góc ở tâm là ${144^o}$ . Người ta uốn hình quạt này thành một hình nón. Tính thể tích của khối nón đó.
Trả lời bởi giáo viên
Đáp án đúng: d
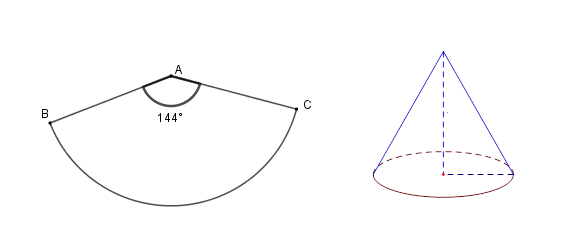
Ta uốn hình quạt \(BAC\) thành hình nón đỉnh \(A\) , đường sinh \(AB = 20\,cm\) .
Khi đó độ dài cung \(BC\) chính là chu vi đáy của hình nón
Ta có độ dài cung \(BC\) là \({l_{BC}} = \dfrac{{\pi .20.144}}{{180}} = 16\pi \)
Khi đó chu vi đáy của hình nón \(C = 2\pi R = 16\pi \Rightarrow R = 8\,cm\) \( \Rightarrow {h^2} = {l^2} - {R^2} = {20^2} - {8^2} \Rightarrow h = 4\sqrt {21} \,cm\)
Thể tích khối nón \(V = \dfrac{1}{3}\pi {.8^2}.4\sqrt {21} = \dfrac{{256\pi \sqrt {21} }}{3}\) \(\left( {c{m^3}} \right)\)
Hướng dẫn giải:
Sử dụng công thức thể tích khối nón $V = \dfrac{1}{3}\pi {R^2}h$

