Câu hỏi:
2 năm trước
Cho mạch điện như hình vẽ:
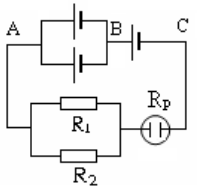
Ba nguồn giống nhau, mỗi nguồn có suất điện động E và điện trở trong r. \({R_1} = 2\Omega ,{R_2} = 6\Omega \). Bình điện phân chứa dung dịch \(CuS{O_4}\) với cực dương bằng đồng và có điện trở \({R_p} = 0,5\Omega \). Sau một thời gian điện phân \(386\) giây, người ta thấy khối lượng của bên cực làm catot tăng lên \(0,636\) gam.
Xác định cường độ dòng điện qua bình điện phân và qua từng điện trở?
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có: \(m = \dfrac{1}{F}.\dfrac{A}{n}.I.t \to I = \dfrac{{m.F.n}}{{A.t}}\)
Thay số: \({I_{tm}} = \dfrac{{0,636.96500.2}}{{64.386}} = 5A\)
Vì bình điện phân mắc nối tiếp\({R_{12}}\)\( \to {I_p} = {I_{12}} = {I_{tm}} = 5A\)
Lại có: \({R_{12}} = \dfrac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{2.6}}{{2 + 6}} = 1,5\Omega \)
\( \to {U_{12}} = {R_{12}}.{I_{12}} = 1,5.5 = 7,5V\)
\( \to {U_1} = {U_2} = {U_{12}} = 7,5V\)
\( \to {I_1} = \dfrac{{{U_1}}}{{{R_1}}} = \dfrac{{7,5}}{2} = 3,75A\)
\( \to {I_2} = \dfrac{{{U_2}}}{{{R_2}}} = \dfrac{{7,5}}{6} = 1,25A\)
Hướng dẫn giải:
- Sử dụng công thức \(m = \dfrac{1}{F}.\dfrac{A}{n}.I.t\)
- Sử dụng công thức mạch song song và nối tiếp:
\(\dfrac{1}{{{R_{//}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}};{I_{//}} = {I_1} + {I_2};{U_{//}} = {U_1} = {U_2}\)
\({R_{nt}} = {R_1} + {R_2};{I_{nt}} = {I_1} = {I_2};{U_{//}} = {U_1} + {U_2}\)
Câu hỏi khác
- Bài tập dòng điện trong chất điện phân - Phương pháp giải bài tập trong chất điện phân lý 11 có lời giải
- Bài tập dòng điện trong kim loại - Phương pháp giải bài tập dòng điện trong kim loại lý 11 có lời giải
- Bài tập dòng điện trong chất bán dẫn lý 11 có lời giải
- Bài tập dòng điện trong chất khí lý 11 có lời giải
- Bài tập dòng điện trong chân không lý 11 có lời giải
