Câu hỏi:
2 năm trước
Cho mạch điện gồm 3 tụ điện \({C_1} = 1\mu F;{C_2} = 1,5\mu F;{C_3} = 3\mu F\) mắc nối tiếp nhau. Đặt vào hai đầu đoạn mạch một hiệu điện thế \({U_{AB}} = 120V\). Hiệu điện thế trên tụ \({C_2}\) có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: b
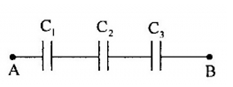
Ta có các tụ mắc nối tiếp
\(\begin{array}{l}\dfrac{1}{{{C_b}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ... + \dfrac{1}{{{C_n}}}\\ = \dfrac{1}{1} + \dfrac{1}{{1,5}} + \dfrac{1}{3} = 2\\ \to {C_b} = 0,5\mu F\end{array}\)
+ Điện tích của bộ tụ: \({Q_b} = {C_b}.{U_{AB}} = 0,{2.10^{ - 6}}.120 = {60.10^{ - 6}}C = 60\mu C\)
Vì các tụ nối tiếp nên: \({Q_1} = {Q_2} = {Q_3} = {Q_b} = 60\mu C\)
+ Hiệu điện thế trên tụ \({C_2}\) là : \({U_2} = \dfrac{{{Q_2}}}{{{C_2}}} = \dfrac{{{{60.10}^{ - 6}}}}{{1,{{5.10}^{ - 6}}}} = 40V\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính điện dung của bộ tụ khi mắc nối tiếp: \(\dfrac{1}{{{C_b}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ... + \dfrac{1}{{{C_n}}}\)
+ Vận dụng biểu thức tính điện lượng: \(Q = CU\)
