Cho lăng trụ đứng ABC.A'B'C' có chiều cao bằng 4, đáy ABC là tam giác cân tại A với AB = AC = 2; \(\angle BAC = {120^0}\). Tính diện tích mặt cầu ngoại tiếp lăng trụ trên.
Trả lời bởi giáo viên
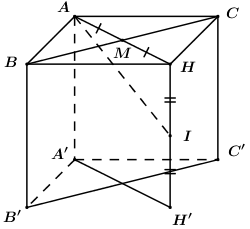
Gọi M là trung điểm của BC, H là điểm đối xứng với A qua M.
Xét tứ giác ABHC có hai đường chéo cắt nhau tại trung điểm mỗi đường và \(AM \bot BC \Rightarrow AH \bot BC\) (do tam giác ABC cân tại A) nên ABHC là hình thoi \( \Rightarrow HB = HC\).
Xét tam giác ABH có AB = BH, \(\angle BAH = \dfrac{1}{2}\angle BAC = {60^0}\) nên là tam giác đều, do đó HA = HB.
Suy ra HA = HB = HC hay H là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi H’ là hình chiếu của A lên (A’B’C’) thì H’ chính là tâm đường tròn ngoại tiếp tam giác A’B’C’, khi đó HH’ là trục của khối lăng trụ đứng.
Gọi I là trung điểm của HH’, ta có IA = IB = IC, IA’ = IB’ = IC’.
Xét tam giác vuông AHI và tam giác vuông A’H’I có: HI = H’I (theo cách dựng), AH = A’H’.
\( \Rightarrow \Delta AHI = \Delta A'H'I\) (2 cạnh góc vuông) \( \Rightarrow IA = IA'\). Do đó A = IB = IC = IA’ = IB’ = IC’ hay I chính là tâm mặt cầu ngoại tiếp khối lăng trụ đứng ABC.A’B’C’.
Ta có AH = AB = 2 (do ABHC là hình thoi) và HH’ = AA’ = 4 nên IH = 2.
Áp dụng định lí Pytago trong tam giác vuông AHI có: \(AI = \sqrt {A{H^2} + H{I^2}} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \).
Suy ra bán kính mặt cầu ngoại tiếp khối lăng trụ là \(R = 2\sqrt 2 \).
Vậy diện tích mặt cầu ngoại tiếp khối lăng trụ là: \({S_{mc}} = 4\pi {R^2} = 4\pi .{\left( {2\sqrt 2 } \right)^2} = 32\pi \).
Hướng dẫn giải:
- Gọi M là trung điểm của BC, H là điểm đối xứng với A qua M. Chứng minh H là tâm đường tròn ngoại tiếp tam giác ABC.
- Gọi H’ là hình chiếu của A lên (A’B’C’), gọi I là trung điểm của HH’, chứng minh I là tâm mặt cầu ngoại tiếp khối lăng trụ đứng.
- Sử dụng định lí Pytago tính bán kính mặt cầu.
- Sử dụng công thức tính diện tích mặt cầu bán kính R là \({S_{mc}} = 4\pi {R^2}\).

