Câu hỏi:
2 năm trước
Cho hình vuông nội tiếp đường tròn $\left( {O;R} \right)$. Chu vi của hình vuông là
Trả lời bởi giáo viên
Đáp án đúng: c
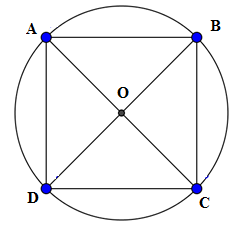
Hình vuông \(ABCD\) nội tiếp đường tròn tâm \(O.\)
Khi đó đường chéo \(BD\) là đường kính của \(\left( O \right)\)
Suy ra \(BD = 2R\)
Xét tam giác \(BDC\) vuông cân tại \(C,\) theo định lý Pytago ta có
$B{C^2} + C{D^2} = B{D^2} \Leftrightarrow 2B{C^2} = 4{R^2} \Rightarrow BC = R\sqrt 2 $
Chu vi hình vuông \(ABCD\) là \(4R\sqrt 2 \)
Hướng dẫn giải:
Xác định đường kính của đường tròn
Định lí Py-ta-go
Câu hỏi khác
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
