Câu hỏi:
2 năm trước
Cho hình vuông $ABCD$ . Trên các cạnh $AB,BC,CD,DA$ lần lượt lấy các điểm $E,F,G,H$ sao cho $AE = BF = CG = DH$ . Tứ giác \(EFGH\) là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: d
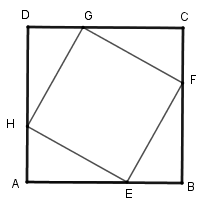
+ Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\) (tính chất).
Mà $AE = BF = CG = DH\,\left( {gt} \right)$ nên \(AB - AE = BC - BF = CD - CG = DA - DH\) hay \(DG = CF = EB = AH\).
Từ đó suy ra \(\Delta AHE = \Delta DGH = \Delta CFG = \Delta EBF\) (c-g-c) nên \(HG = GF = HE = EF\).
Vì \(HG = GF = HE = EF\) nên tứ giác \(EFGH\) là hình thoi.
+ Vì \(\Delta AHE = \Delta BEF\,\left( {cmt} \right) \Rightarrow \widehat {AHE} = \widehat {BEF}\) (hai góc tương ứng) mà \(\widehat {AHE} + \widehat {HEA} = 90^\circ \Rightarrow \widehat {BEF} + \widehat {HEA} = 90^\circ \)
Từ đó \(\widehat {HEF} = 180^\circ - \left( {\widehat {HEA} + \widehat {BEF}} \right) = 180^\circ - 90^\circ = 90^\circ \) .
Hình thoi \(EFGH\) có \(\widehat {HEF} = 90^\circ \) nên \(EFGH\) là hình vuông.
Hướng dẫn giải:
Bước 1: Ta chứng minh \(DG = CF = EB = AH\). Từ đó suy ra \(\Delta AHE = \Delta DGH = \Delta CFG = \Delta EBF\) nên \(HG = GF = HE = EF\) . Do đó tứ giác \(EFGH\) là hình thoi.
Bước 2: Chứng minh góc \(\widehat {HEF} = 90^\circ \) để suy ra \(EFGH\) là hình vuông.
Câu hỏi khác
- Đề kiểm tra giữa học kì 2 - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 4 Toán 8 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 3 Toán 8 có lời giải chi tiết
