Câu hỏi:
3 năm trước
Cho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi.
Trả lời bởi giáo viên
Đáp án đúng: a
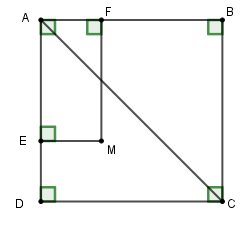
Tứ giác \(AFME\) có: \(\widehat A = \widehat {AFM} = \widehat {AEM} = 90^\circ \) nên \(AEMF\) là hình chữ nhật.
Để hình chữ nhật \(AEMF\) là hình vuông thì \(AM\) là phân giác \(\widehat {EAF}\).
Mà ta lại có: \(AC\) là phân giác \(\widehat {DAB}\) (do \(ABCD\) là hình vuông).
Nên suy ra \(M \in AC\).
Hướng dẫn giải:
Dựa vào hai dấu hiệu nhận biết: “Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông”
Sử dụng tính chất hình vuông.