Câu hỏi:
2 năm trước
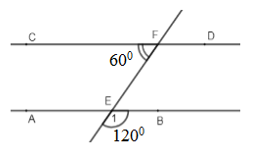
Cho hình vẽ:
Biết \(\widehat {CFE} = {60^0};\,\widehat {{E_1}} = {120^0}.\) Chọn câu sai.
Trả lời bởi giáo viên
Đáp án đúng: d
Vì \(\widehat {{E_1}}\) và \(\widehat {BEF}\) là hai góc kề bù.
\( \Rightarrow \widehat {{E_1}} + \widehat {BEF} = {180^0} \Rightarrow \widehat {BEF} = {180^0} - \widehat {{E_1}} = {180^0} - {120^0} = {60^0}\)
\( \Rightarrow \widehat {BEF} = \widehat {CFE} = {60^0}\).
Mà \(\widehat {BEF}\)và \(\widehat {CFE}\) là hai góc so le trong nên suy ra \(AB//C{\rm{D}}\) (dấu hiệu nhận biết hai đường thẳng song song).
Do đó cả A, B, C đúng.
Đáp án sai là D.
Hướng dẫn giải:
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b,\) trong các góc tạo thành có \(1\) cặp góc so le trong bằng nhau thì \(a//b\).
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
